Example of Model of Fe-Terephthalate Ordering on Cu(100) : Monte Carlo method

Here we provide an example of applying the Monte Carlo method to simulate the self-assembly of two-dimensional metal-organic network of Fe-Terephthalate on Cu(100) surface. In this example we use the standard Metropolis Monte Carlo simulation in grand canonical ensemble.

Model

We used the generalized lattice model of adsorption monolayers, a mathematically rigorous description of which is given in the paper [1]. A square lattice with parameter a is used as a model of the copper surface. The lattice sites represent the hollow sites between four copper atoms on the Cu(100) surface. Please download the archive TPA_Fe_Cu100.zip containing the chemical structures of adsorption complexes and pair configurations of TPA and Fe in the considered lattice model. Additionally, the archive includes an energy file providing the energy values for each pair configuration. A detailed description of the model can be found in the paper [2].

Using scanning tunneling microscopy (STM), Lingenfelder et al. [3] and Tait et al. [4] observed the metal−organic networks in the monolayer of TPA molecules and Fe atoms on the Cu(100) surface. When the Fe−TPA ratio is close to ∼0.8−1.0 Fe atoms per TPA molecule, the “ladder phase” emerged in the adsorption layer. This structure comprises the perpendicular zigzag rows of TPA molecules separated by Fe atoms. As the Fe−TPA ratio increased up to 1.2, the “single-row phase” appeared in the monolayer. The script can be used to simulate the self-assembly of both structures.

Code for Monte Carlo Simulation

Please have a look at the following script mc_TPA_Fe_Cu100.py and read below what the script does.

from susmost import load_lattice_task
from susmost import mc

lt = load_lattice_task('./')

# Conditions for the single-row phase (C): muTPA = 25, muFe = 25, L = 24
# Conditions for the ladder phase (A): muTPA = 15, muFe = 35, L = 16
# Fadeeva A.I. et al. // J. Phys. Chem. C. 2019. Vol. 123, № 28. P. 17265.

muTPA = 15.
muFe = 35.
lt.set_ads_energy('TPA', muTPA)       # kJ/mol
lt.set_ads_energy('Fe', muFe) # kJ/mol

L = 16                        # lattice size
T = [400, 500, 700, 1000]             # K
kB = 0.0083 # kJ/(mol*K)
m = mc.make_metropolis(lt, L, T, kB)
mc.run(m, log_periods_cnt=20, log_period_steps = 1000*m.cells_count, relaxation_steps = 500000*m.cells_count, \
    traj_fns = ["muTPA={}_muFe={}_T={}.xyz".format(muTPA, muFe, temp) for temp in T])
mc.stat_digest(m)

load_lattice_task and mc are the modules of the susmost general library required for setting up the structure of the lattice model and applying the Monte Carlo methods to simulate that. muTPA and muFe are the state energies of the TPA and Fe adsorption complexes, in kJ/mol. Physical meaning of state energy \(\mu\) is the energy change caused by formation of the corresponding adsorption complex on a clean surface, for example on adsorption of a molecule from an equilibrium gas phase (that is close to the term “chemical potential”).

lt.set_ads_energy sets the state energies of the TPA and Fe adsorption complexes.

In this example we perform the Monte Carlo simulation using the hyperparallel tempering technique to speed up the convergence to the desired, but only for 4 temperatures. make_metropolis function creates a task m for Monte Carlo simulation. Here we run the m simulation with relaxation time - 500 000 Monte Carlo steps (MCS) and 20 000 MCS for thermal averaging over the 20 points.

stat_digest prints summary on sample statistics.

Results: Fe-Terephthalate Ordering on Cu(100)

When the chemical potentials of TPA and Fe equal to 25 and 25, correspondingly, the single-row phase appears in the adlayer. Fig. 1 shows the typical result of the simulation.

Fig. 1. Single-row phase in the Fe-Terephthalate adlayer on Cu(100).

The ladder phase is formed at other values of the chemical potentials of TPA and Fe (Fig. 2).

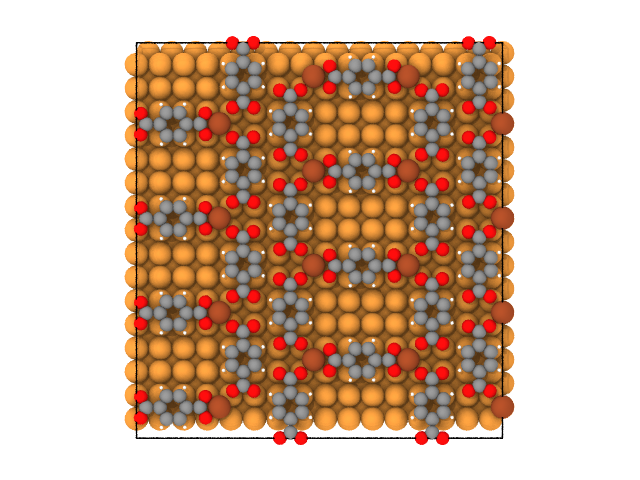
Fig. 2. Ladder phase in the Fe-Terephthalate adlayer on Cu(100) at \(\mu_{TPA} = 15\) and \(\mu_{Fe} = 35\).

References

[1]

S.S. Akimenko, V.A. Gorbunov, A.V. Myshlyavtsev, P.V. Stishenko, Generalized lattice-gas model for adsorption of functional organic molecules in terms of pair directional interactions, Physical Review E. 93 (2016) 062804. https://doi.org/10.1103/PhysRevE.93.062804.

[2]

A.I. Fadeeva, V.A. Gorbunov, P.V. Stishenko, A.V. Myshlyavtsev, Model of Fe-Terephthalate Ordering on Cu(100), J. Phys. Chem. C. 123 (2019) 17265–17272. https://doi.org/10.1021/acs.jpcc.9b02834.

[3]

M.A. Lingenfelder, H. Spillmann, A. Dmitriev, S. Stepanow, N. Lin, J.V. Barth, K. Kern, Towards Surface-Supported Supramolecular Architectures: Tailored Coordination Assembly of 1,4-Benzenedicarboxylate and Fe on Cu(100), Chemistry - A European Journal. 10 (2004) 1913–1919. https://doi.org/10.1002/chem.200305589.

[4]

S.L. Tait, Y. Wang, G. Costantini, N. Lin, A. Baraldi, F. Esch, L. Petaccia, S. Lizzit, K. Kern, Metal−Organic Coordination Interactions in Fe−Terephthalic Acid Networks on Cu(100), Journal of the American Chemical Society. 130 (2008) 2108–2113. https://doi.org/10.1021/ja0778186.