SUrface Science MOdeling and Simulation Toolkit
SuSMoST is a set of computer programs and libraries that are intended to support studies of surfaces with emphasize on adsorption systems and phase transitions. Currently SuSMoST is being actively developed by staff of Computational Chemistry Laboratory of Omsk State Technical University (OmSTU). SuSMoST development is supported by Russian Science Foundation (project No 17-71-20053 for 2017-2020 years). SuSMoST emerged from the decade of computational studies of physico-chemical processes on surfaces conducted by the scientific group lead by Alexander V. Myshlyavtsev in OmSTU.
Citing SuSMoST
SuSMoST: Surface Science Modeling and Simulation Toolkit, S. S. Akimenko, G. D. Anisimova, A. I. Fadeeva, V. F. Fefelov, V. A. Gorbunov, T. R. Kayumova, A. V. Myshlyavtsev, M. D. Myshlyavtseva, and P. V. Stishenko,
Journal of Computational Chemistry, 2020. DOI: 10.1002/jcc.26370.
Mentions in the media:

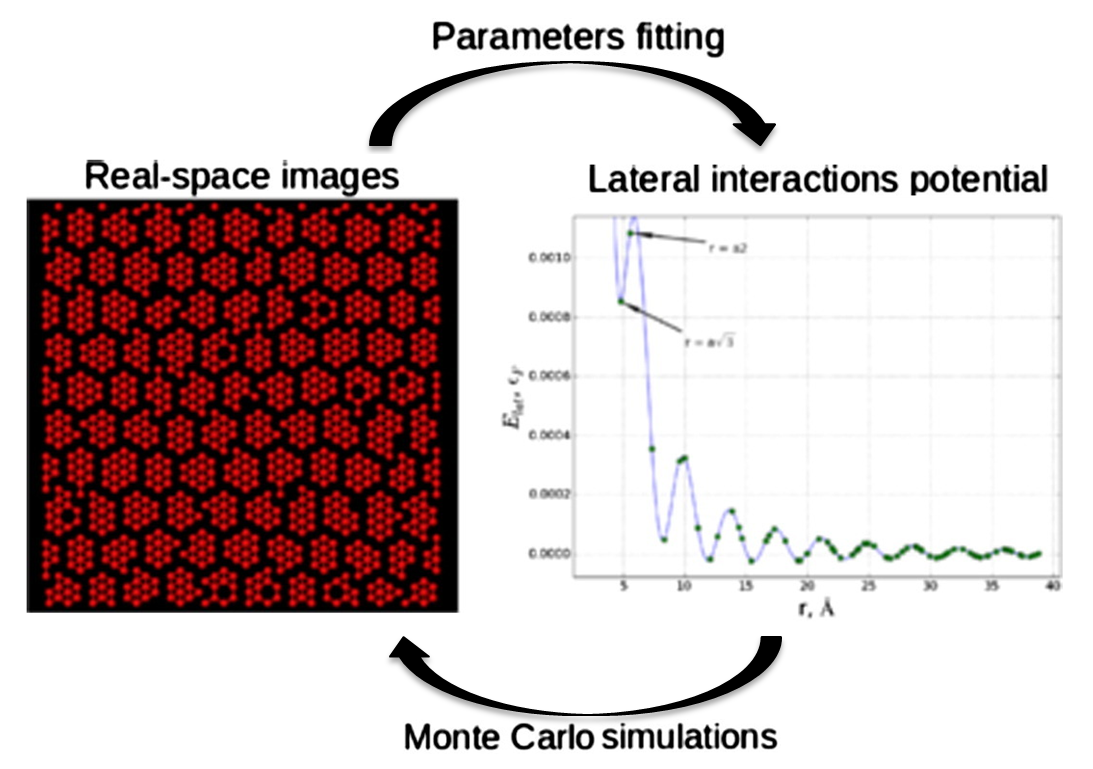
Abstract: A simple lattice model of the orientational ordering in organic adsorption layers that considers the directionality of intermolecular interactions is proposed. The symmetry and the number of rotational states of the adsorbed molecule are the main parameters of the model. The model takes into account both the isotropic and directional contributions to the molecule-molecule interaction potential. Using several special cases of this model, we have shown that the tensor renormalization group (TRG) approach can be successfully used for the analysis of orientational ordering in organic adsorption layers with directed intermolecular interactions. Adsorption isotherms, potential energy, and entropy have been calculated for the model adsorption layers differing in the molecule symmetry and the number of rotational states. The calculated thermodynamic characteristics show that entropy effects play a significant role in the self-assembly of dense phases of the molecular layers. All the results obtained with the TRG have been verified by the standard Monte Carlo method. The proposed model reproduces the main features of the phase behavior of the real adsorption layers of benzoic, terephthalic, and trimesic acids on a homogeneous surface of metal single crystals and graphite. View article
GAZETA.RU: "A model was developed to predict new organometallic structures"
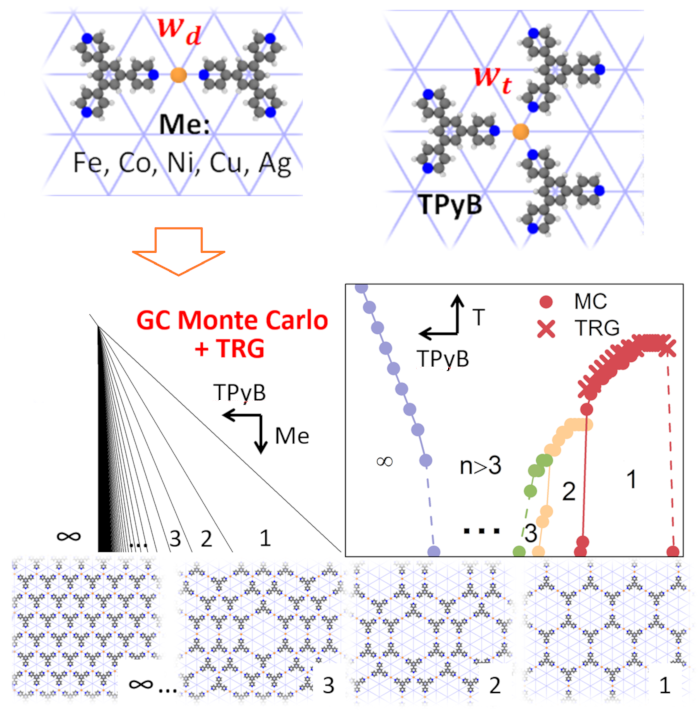
Abstract: Supramolecular coordination self-assembly on the solid surface offers great possibilities for creating nanostructures and thin films with unique physicochemical properties. In this work, we present a simple lattice model based on competitive coordination motifs that enables prediction of the phase behavior and thermal stability of metal–organic networks consisting of 1,3,5-tris(pyridyl)benzene (TPyB) and transition metals on Au(111) surface. The main parameter of the model is the ratio between the energies of the two-fold and three-fold metal–ligand coordination defined by the type of the metal center... View article

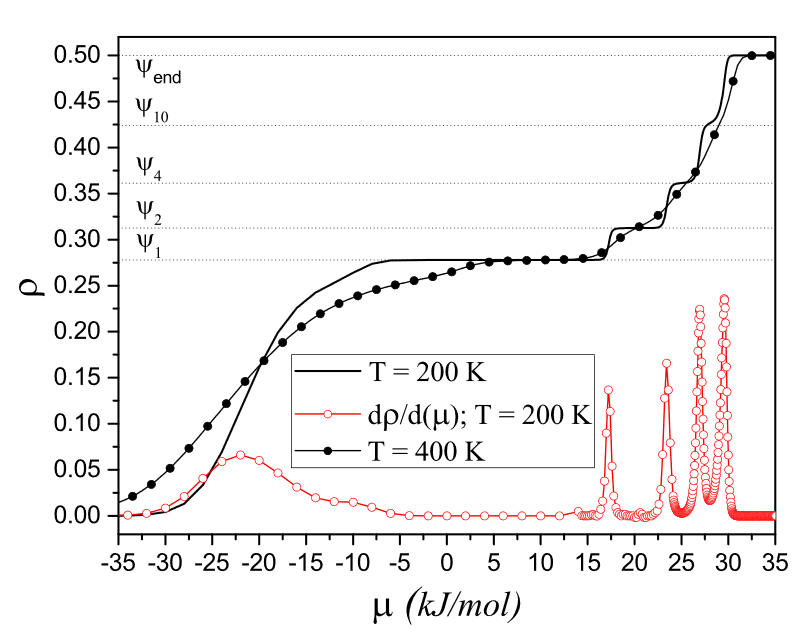
Abstract: High accuracy and performance of the tensor renormalization group (TRG) method have been demonstrated for the model of hard disks on a triangular lattice. We considered a sequence of models with disk diameter ranging from a to 2√3a, where a is the lattice constant. Practically, these models are good for approximate description of thermodynamics properties of molecular layers on crystal surfaces. Theoretically, it is interesting to analyze if and how this sequence converges to the continuous model of hard disks. The dependencies of the density and heat capacity on the chemical potential were calculated with TRG and transfer-matrix (TM) methods. We benchmarked accuracy and performance of the TRG method comparing it with TM method and with exact result for the model with nearest-neighbor exclusions (1NN). The TRG method demonstrates good convergence and turns out to be superior over TM with regard to considered models... View article

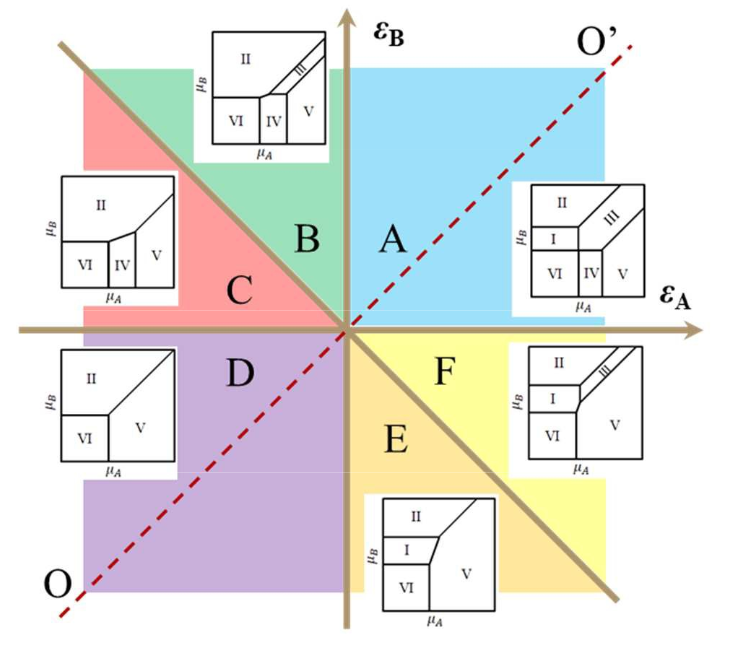
Abstract: In this paper, a complete analysis of the phase diagrams of the model of adsorption of a binary gas mixture on a square lattice in the ground state for all sets of near undirected interactions between particles was performed. Using the principle of minimum of a large thermodynamic potential in a stable phase, the partition of the model parameter space (the energies of lateral interactions) into regions differing by the type of the phase diagram was constructed. Also, for some regions, partial and total coverages as functions of chemical potentials of the gases were calculated through transfer-matrix method and presented. The work is an extension of the work (Fefelov in Phys Chem Chem Phys 20(15): 10359–10368, 2018). View article
GAZETA.RU: Scientists have come up with how to create triangular bricks using self-assembling molecules"
Abstract: The model of dimers adsorption on hexagonal lattice with different orientations to surface and hard-spheres lateral interactions has been studied at nonzero temperature. The transfer-matrix method was used as the main one and the Monte Carlo method was used for checking of some extreme cases. Adsorption isotherms, dependencies of the entropy from the density of the adsorption layer and of the energy from the system temperature at certain points of the phase space, were computed. It was found that at least the first ten phases of the ground state still persist at nonzero temperatures. View article
Abstract: Complete analysis of phase behavior of an adsorption model of a binary gas mixture on a square lattice was carried out for all possible sets of lateral interactions between nearest adsorbed molecules of the same type and no interaction between adsorbed molecules of different types. The model was completely investigated in the ground state, and it was shown that the phase behavior of the system is conserved at finite temperatures by means of a transfer matrix method. View article
Recent studies conducted with SuSMoST:
J. Phys. Rev. E, 2023. DOI: 10.1103/PhysRevE.108.014133.
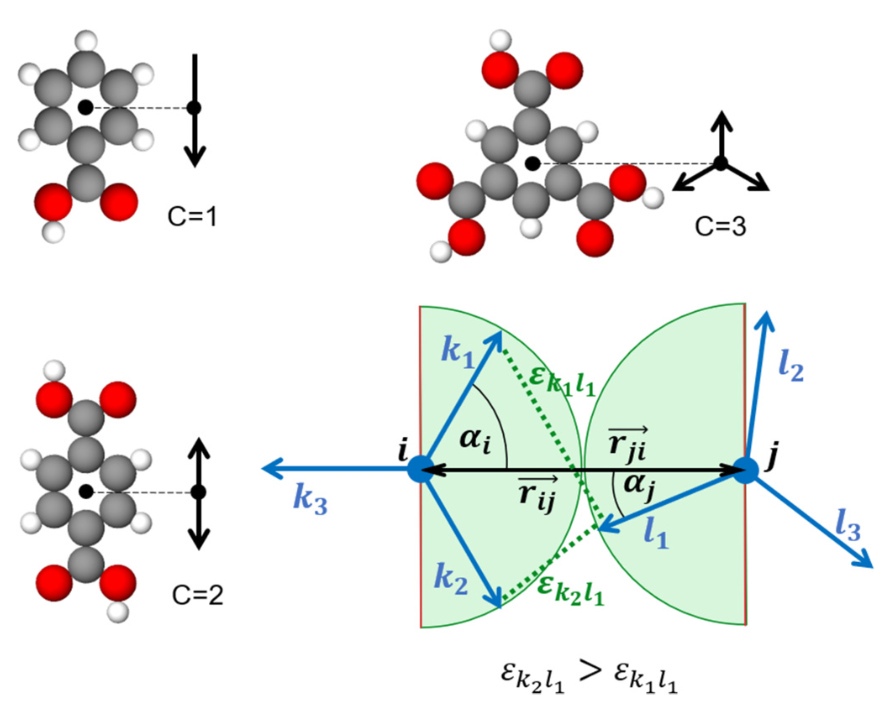
J. Phys. Rev. E, 2023. DOI: 10.1103/PhysRevE.107.054116.
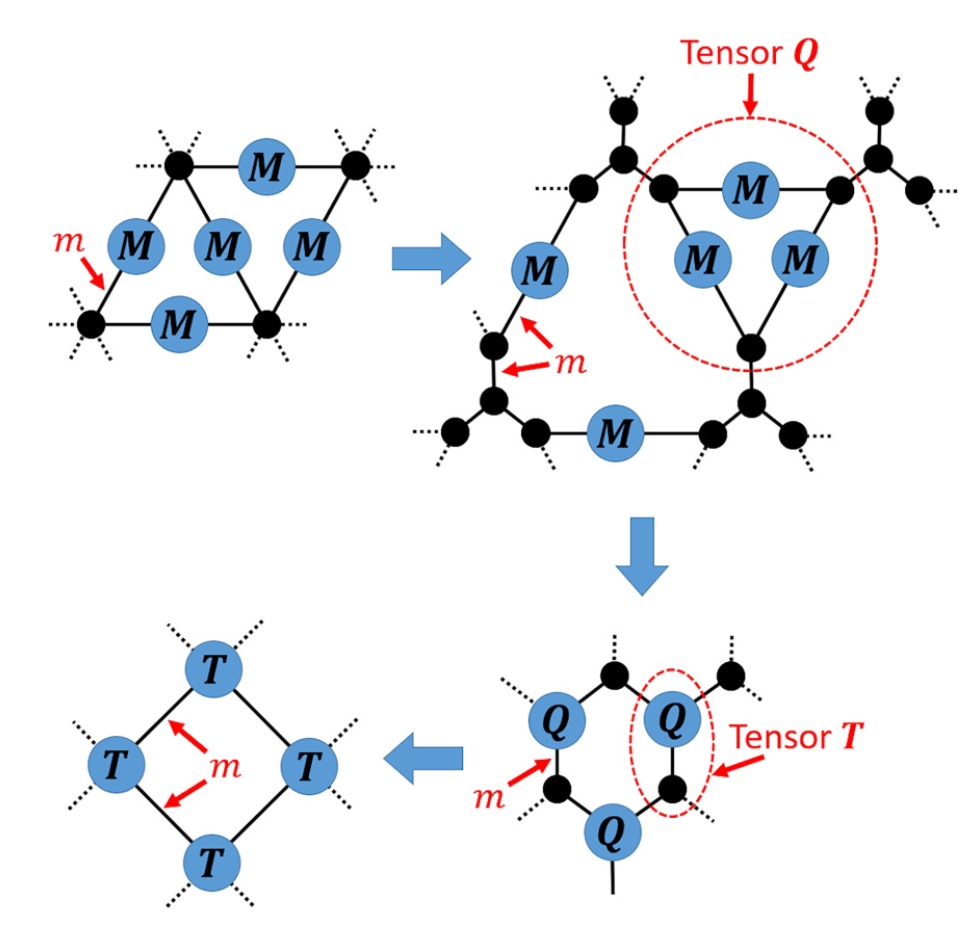
J. Phys. Rev. E, 2022. DOI: 10.1103/PhysRevE.105.044104.
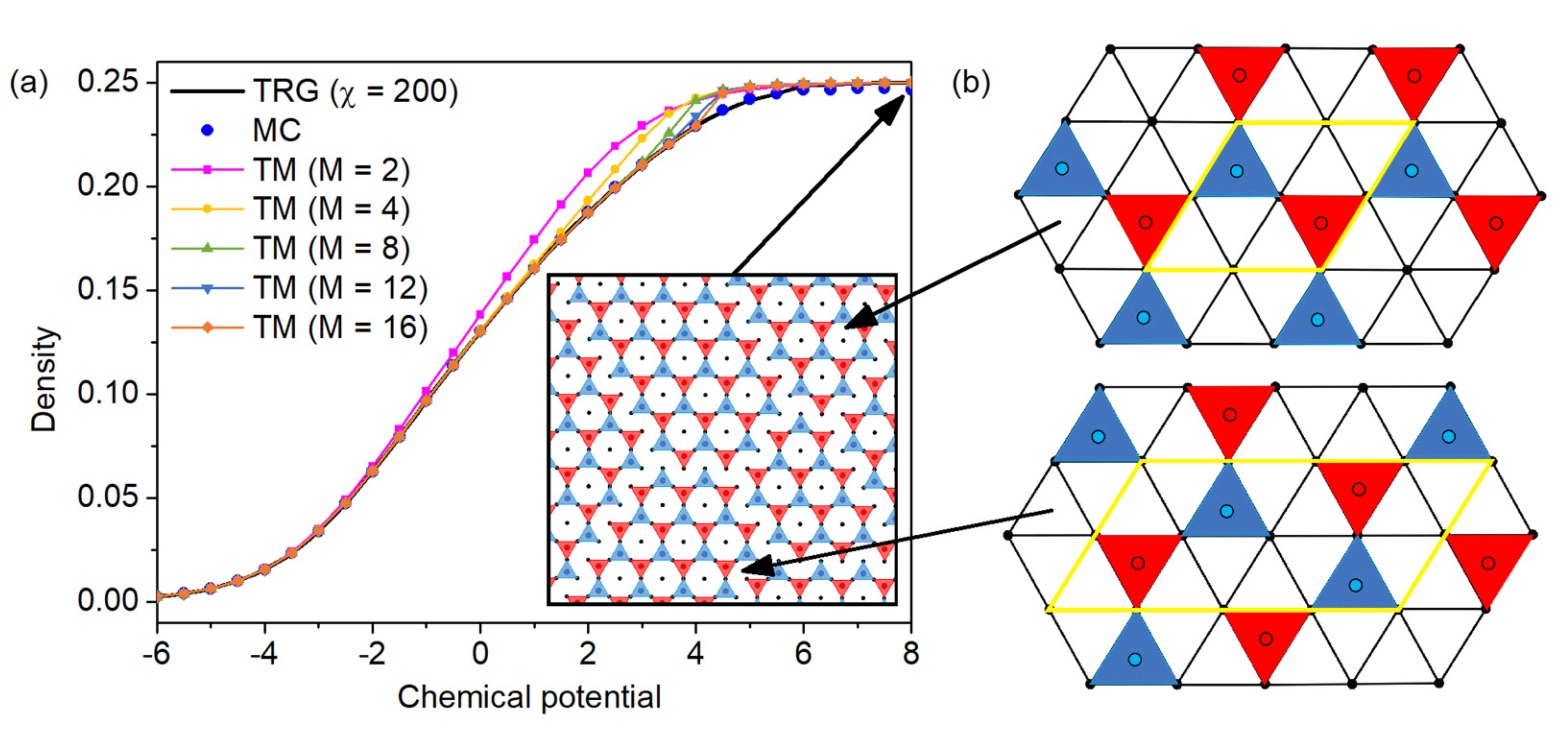
J. Phys. Rev. E, 2022. DOI: 10.1039/D2ME00199C.
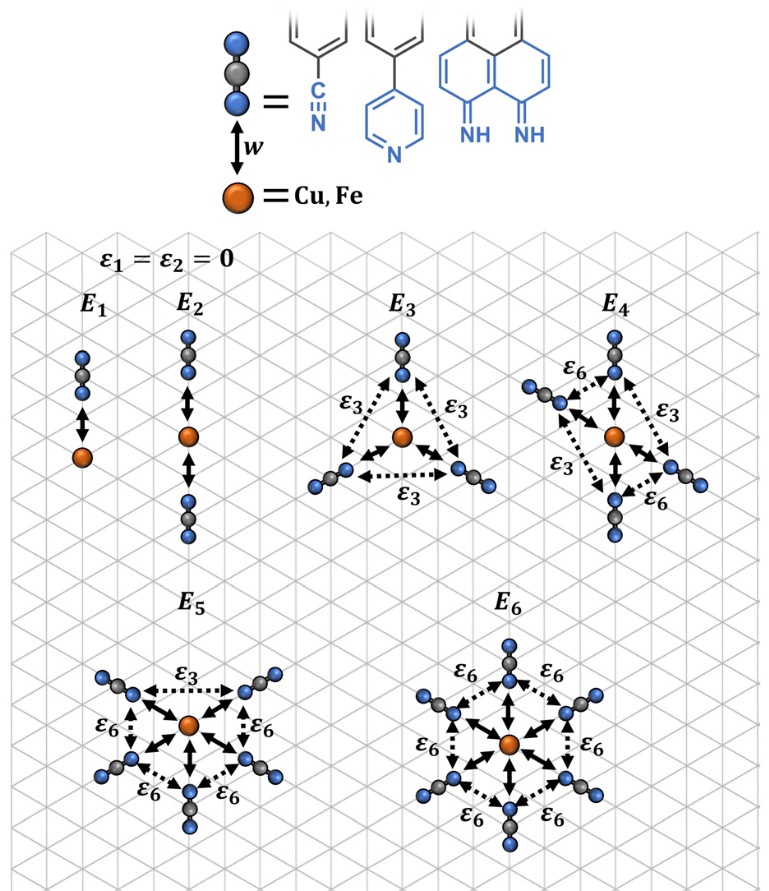
J. Phys. Rev. E, 2022. DOI: 10.1016/j.apsusc.2022.153834.
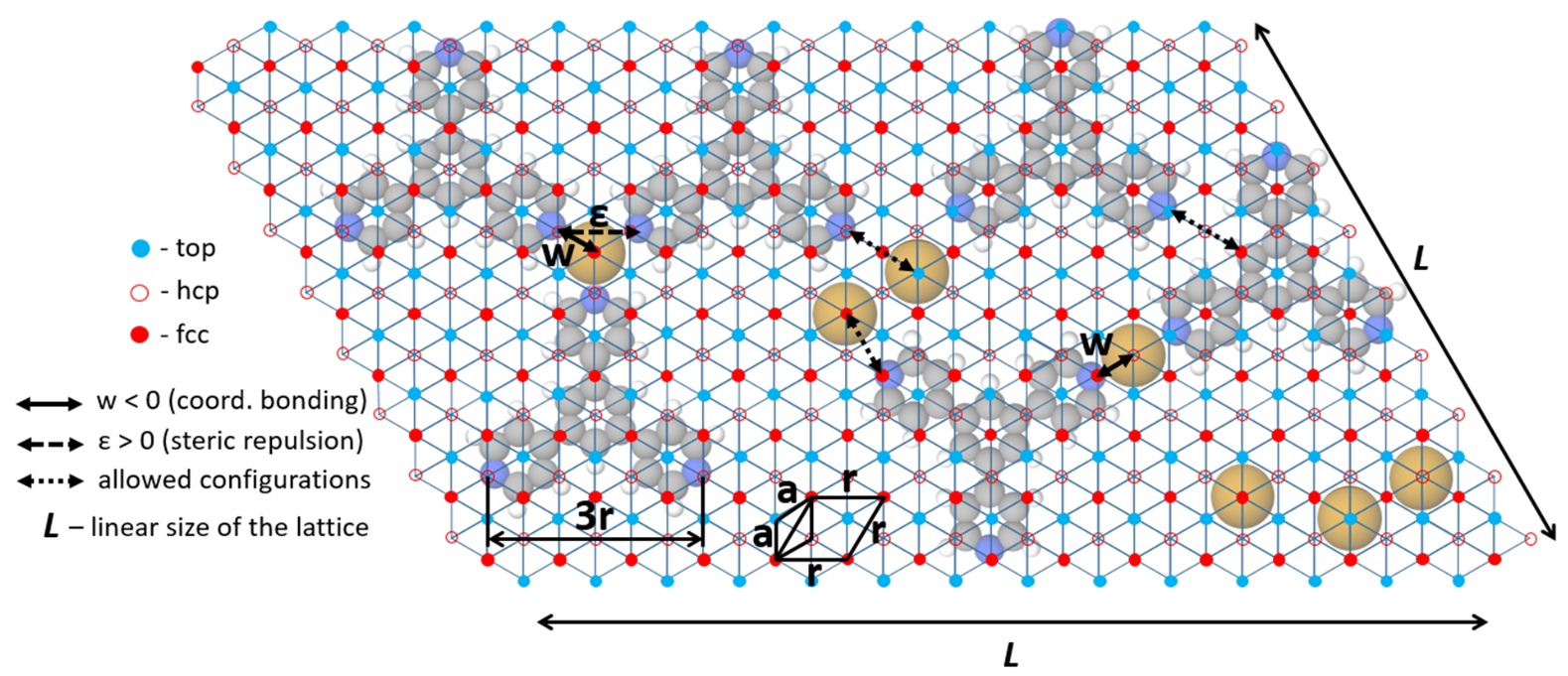
J. Phys. Rev. E, 2021. DOI: 10.1016/j.susc.2021.121984.
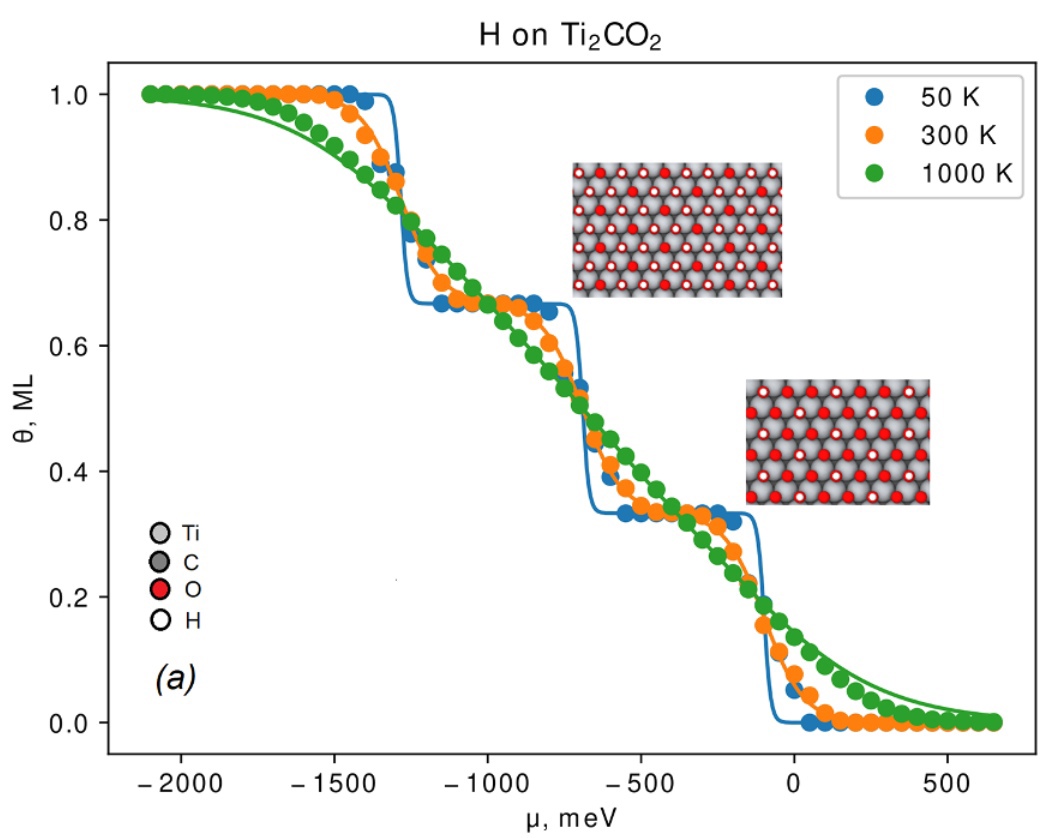
J. Phys. Rev. E, 2021. DOI: 10.1039/D1CP03111B.
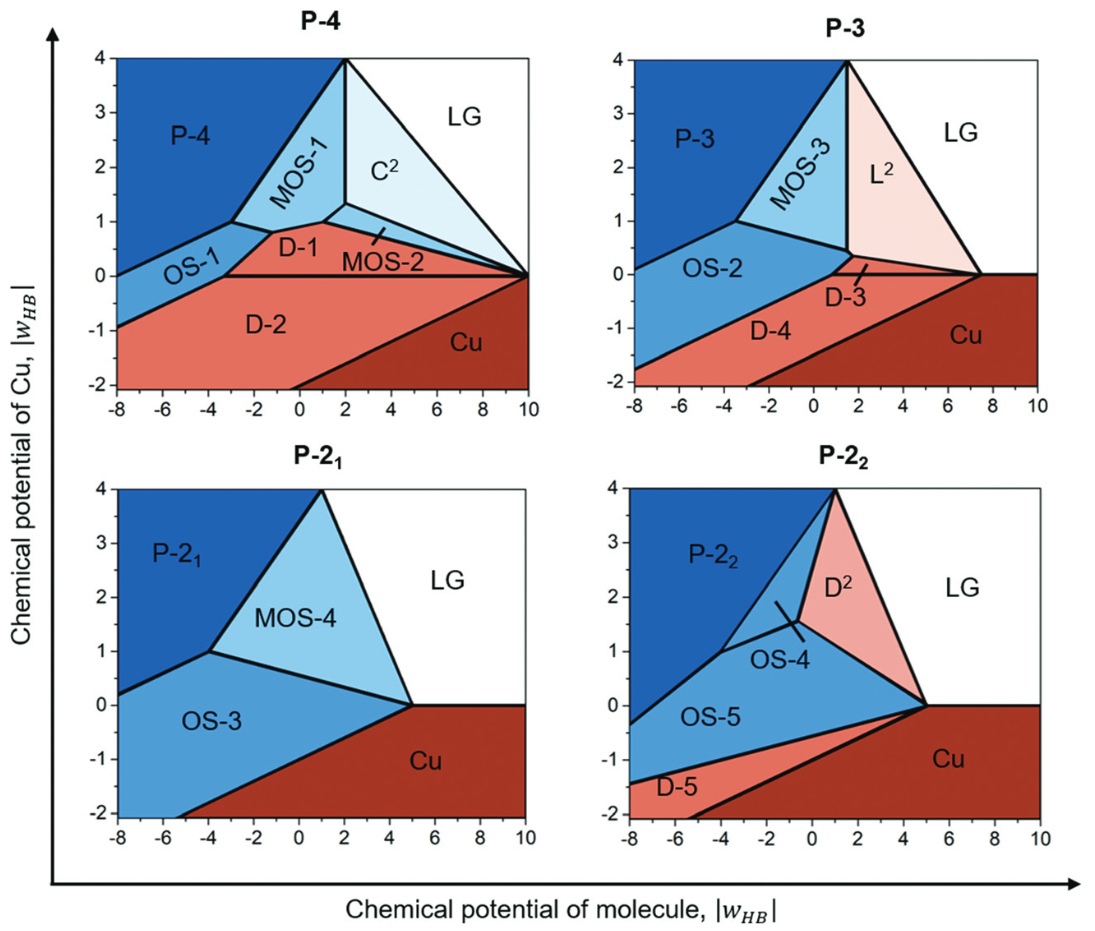
J. Phys. Chem. C, 2021. DOI: 10.1016/j.apsusc.2021.148989.
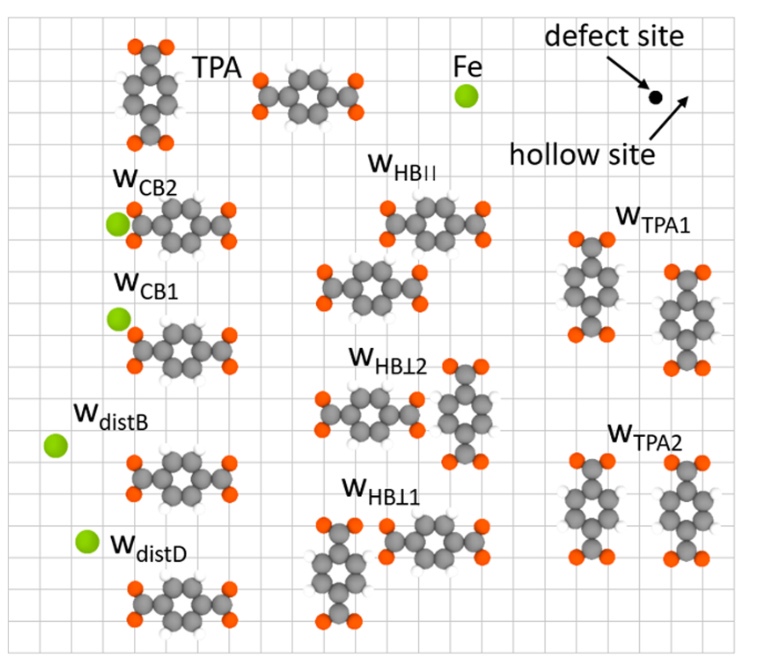
J. Phys. Chem. C, 2020. DOI: 10.1021/acs.jpcc.0c02527.

Physica A, 2020. DOI: 10.1016/j.physa.2020.124919.
Physical Review E, 2019. DOI: 10.1103/PhysRevE.100.022108.

J. Phys. Chem. C, 2019. DOI: 10.1021/acs.jpcc.9b02834.
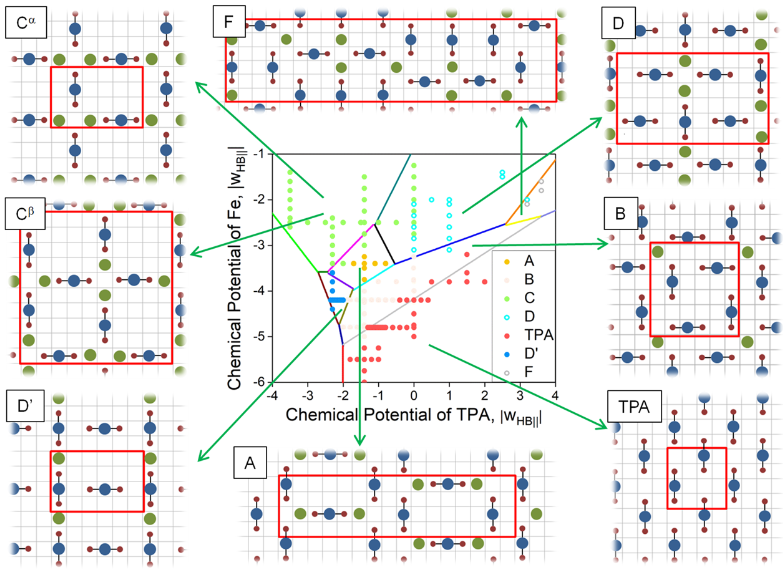
ChemRxiv, 2019. DOI: 10.26434/chemrxiv.8068307.v1.
Adsorption, 2019. DOI: 10.1007/s10450-019-00043-3.

View PDF
AIP Conference Proceedings, 2018. DOI: 10.1063/1.5051853.
AIP Conference Proceedings, 2018. DOI: 10.1063/1.5051848.
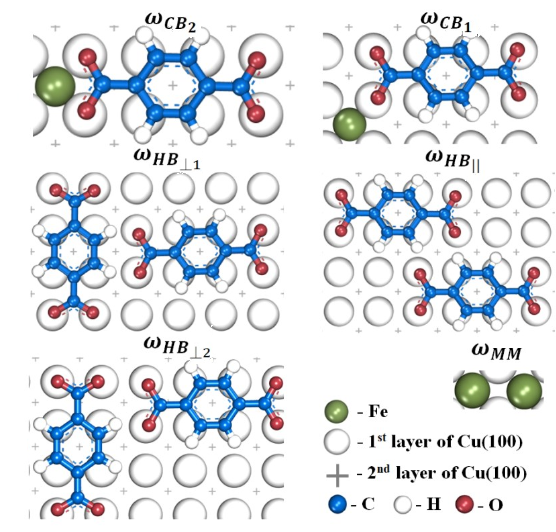
Physical Chemistry Chemical Physics, 2018. DOI: 10.1039/C7CP08426A.

Physical Review B, 2018. DOI: 10.1103/PhysRevB.97.085408.

Physical Chemistry Chemical Physics, 2017. DOI: 10.1039/C7CP01863K.
Surface Science, 2017. DOI: 10.1016/j.susc.2017.06.016.
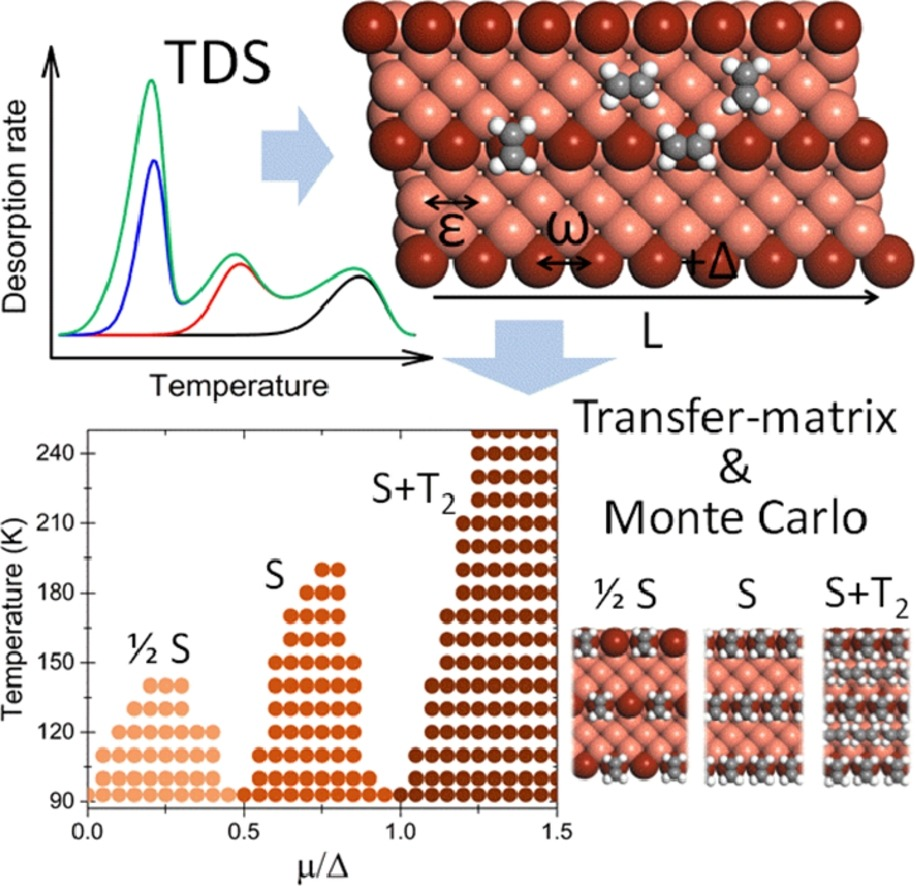
Physical Review E, 2016. DOI: 10.1103/PhysRevE.93.062804.
Adsorption, 2016. DOI: 10.1007/s10450-015-9753-x.
Surface Science, 2015. DOI: 10.1016/j.susc.2015.08.018.